📌 Introducción
El movimiento parabólico es un caso especial de movimiento bidimensional en el cual un objeto sigue una trayectoria curva debido a la acción de la gravedad. En este artículo, exploraremos la teoría del movimiento parabólico, sus ecuaciones fundamentales y presentaremos una simulación interactiva que permite visualizar cómo varía la trayectoria de un proyectil al modificar sus condiciones iniciales.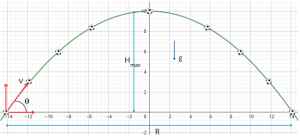
📖 Conceptos Fundamentales
El movimiento parabólico se descompone en dos componentes independientes:
✅ Movimiento horizontal (MRU – Movimiento rectilíneo uniforme):
- La velocidad es constante.
- No hay aceleración en ausencia de resistencia del aire.
✅ Movimiento vertical (MRUV – Movimiento rectilíneo uniformemente variado):
Este análisis nos permite describir matemáticamente la trayectoria del proyectil.
- Acelerado por la gravedad (-9.81 m/s² en la Tierra).
- Alcanza una altura máxima cuando la velocidad vertical es cero.
📊 Ecuaciones del Movimiento Parabólico
📌 Posición en función del tiempo
Las ecuaciones que describen la posición del proyectil en función del tiempo son:$$ x = v_0 \cos(\theta) t \!$$
$$ y = v_0 \sin(\theta) t – \frac{1}{2} g t^2 \!$$
📌 Altura máxima:
$$ H_{max} = \frac{(v_0^2 \sin^2(\theta))}{2g} $$
📌 Alcance máximo:
$$ R = \frac{(v_0^2 \sin(2\theta))}{g} $$
📌 Tiempo de vuelo:
$$ T = \frac{2 v_0 \sin(\theta)}{g} $$
Estas ecuaciones permiten predecir la trayectoria del proyectil en cualquier instante.
🔬 Ejemplo Práctico con Simulación Interactiva
Para comprender mejor cómo afectan la velocidad inicial y el ángulo de lanzamiento a la trayectoria de un proyectil, hemos desarrollado una simulación interactiva.📌 ¿Cómo usar la simulación?
- 1️⃣ Introduce un valor para la velocidad inicial (m/s).
- 2️⃣ Ingresa los valores de ángulo de lanzamiento para comparar dos trayectorias.
- 3️⃣ Presiona «Generar Gráfica» y observa la trayectoria del proyectil.
