Diseño de ménsula de concreto

En la construcción de un centro comercial en la ciudad, no se logra compatibilizar adecuadamente los planos estructurales y arquitectónicos. Como resultado, la armadura de acero no coincide con otro tijeral para su unión, sino con una columna de concreto. La solución propuesta es realizar una ménsula sobre la columna. Para este procedimiento se emplea la norma ACI 318-19.

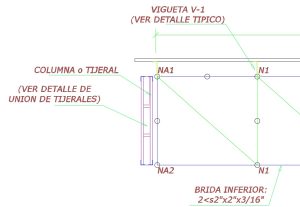
Fig. 1 Detalles del tijeral metálico

Las acciones de las cargas sobre la ménsula son:

\(F_y = 14710\ \text{N}\)

\(F_x = 4010\ \text{N}\)

1. Según el capítulo 16.5.2.4, para concreto de densidad normal, las dimensiones de la ménsula se limitan según las siguientes tres ecuaciones, de manera que \(V_u / \phi\) no exceda el menor de:

   • \(\dfrac{\dfrac{V_u}{\phi}}{0.2 (f’c) (b_w) d} \Rightarrow d \geq \dfrac{14710\ \text{N}}{0.75(0.2)(27.5\ \text{MPa})(350\ \text{mm})} = 10.2\ \text{mm}\)

   • \(\dfrac{\dfrac{V_u}{\phi}}{(3.3 +0.08 f’c)(b_w)d} \Rightarrow d \geq \dfrac{14710\ \text{N}}{0.75(3.3 + 0.08(27.5\ \text{MPa}))(350\ \text{mm})} = 10.2\ \text{mm}\)

   • \(\dfrac{\dfrac{V_u}{\phi}}{11(b_w)d} \Rightarrow d \geq \dfrac{14710\ \text{N}}{0.75(11)(350\ \text{mm})} = 5.1\ \text{mm}\)

   El valor mínimo es de 10.2 mm, pero según la relación indicada en 16.5.1.1:

   \(a_v \leq d \Rightarrow\) probamos con un valor de \(d = 480\ \mathrm{mm}\)

2. La altura de la cara exterior de la ménsula, según la imagen R16.5.1a, debe ser mayor o igual a 0.5d, por lo que:

   \(h_1 = 240\ \text{mm}\)

3. Se usa un recubrimiento de 40 mm según la tabla 20.5.1.3.1.
4. Se verifica que:

   \(N_{uc} \leq V_n \Rightarrow 4010\ \text{N} \leq 14710\ \text{N}\)

5. El coeficiente de fricción asumido según la tabla 22.9.4.2, es de:

   \(\mu = 1\)

6. El área requerida para el esfuerzo cortante por fricción se calcula según 22.9.4.2:

   \(A_{vf} = \dfrac{V_u}{\phi \mu f_y} = \dfrac{14710}{0.75(1)(412)} = 47.6\ \mathrm{mm}^2\)

7. Según R16.5.3.1, el momento:

   \(M_u = V_n a_v + N_{uc} (h – d)\)

   \(M_u = 14710 (200) + 4010 (40) = 3102400\ \text{Nmm}\)

8. El área de acero de refuerzo en la ménsula:

   \(A_f = \dfrac{M_u}{\phi f_y 0.9 d}\)

   \(A_f = \dfrac{3102400}{0.75(412)(0.9)(480)} = 23.2\ \mathrm{mm}^2\)

9. Según 16.5.4.3, el área de refuerzo en una ménsula que resiste la fuerza de restricción mayorada:

   \(A_n = \dfrac{N_{uc}}{\phi f_y}\)

   \(A_n = \dfrac{4010}{0.75(412)} = 13.1\ \mathrm{mm}^2\)

10. Según 16.5.5.1, el área de refuerzo principal a tracción en una ménsula:
    • \(A_f + A_n \Rightarrow 23.2 + 13.1 = 36.3\ \mathrm{mm}^2\)

    • \(\dfrac{2}{3} A_{vf} + A_n \Rightarrow \dfrac{2}{3}(47.6) + 13.1= 44.8\ \mathrm{mm}^2\)

    • \(0.04 \dfrac{f’_c}{f_y} (b_w d) \Rightarrow 0.04 (\dfrac{27.5}{412})(350)(480) = 186.9\ \mathrm{mm}^2\)

    El valor máximo a tomar es \(A_{sc} = 448.5\ \mathrm{mm}^2\) Para cumplir con el requisito se deben usar 4 barras de \(\phi = 12.7\ \mathrm{mm}\), teniendo un área de:

    \(A_{sc} = 4\dfrac{(\pi)(12.7^2)}{4} = 506.7\ \mathrm{mm}^2 > 448.5\ \mathrm{mm}^2 \)

11. El área total de estribos cerrados o paralelos al refuerzo principal, según 16.5.5.2, debe ser al menos:

    \(A_h = 0.5 (A_{sc} – A_n) = 0.5(506.7 – 13.1) = 246.8\ \mathrm{mm}^2\)

    Usaremos 4 barras de \(\phi = 9.5\ \mathrm{mm}\), teniendo un área de:

    \(A_h = 4\dfrac{(\pi)(9.5^2)}{4} = 283.5\ \mathrm{mm}^2 > 246.8\ \mathrm{mm}^2 \)

    Según 16.5.6.6, los estribos cerrados deben espaciarse de tal manera que \(A_h\) quede distribuido dentro de los \(2\dfrac{d}{3}\) adyacentes al refuerzo principal de tracción.

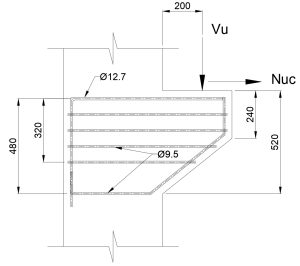
Fig. 2 Detalle de la ménsula